Suspension of Antiviral Treatment for Alleviating Drug Resistance during Influenza Pandemics
Antiviral stockpiling is one of the actions taken by many countries and the World Health Organization (WHO) for preparation of the next influenza pandemic. Drug stockpiling, vaccine development and policies for controlling spread of viruses are essential in combating influenza pandemics1. However, the efficacy of antiviral treatment will be greatly reduced if antiviral resistance develops during the pandemic. The current study evaluates the outcomes of suspension on antiviral treatment in order to alleviate the spread of resistance during an influenza pandemic.
Influenza Pandemics
A pandemic is an epidemic that spreads widely through populations across large areas or even in a worldwide scale. Influenza is one of the diseases that has previously caused pandemics and is currently of concern for its potential of giving rise to pandemics in the near future. During viral replication, influenza A viruses are subjected to high level of mutations leading to changes in haemagglutinins (H) and neuraminidases (N). These antigenic changes, known as antigenic drift, can be slight and occur annually resulting in seasonal influenza2. In some changes, known as antigenic shift, the level of mutation is so high that human population is immunologically naïve to the new viral strain. Hence, the viral strain can spread throughout human populations leading to pandemic influenza3.
The Worst Scenario in Influenza Pandemics
Oseltamivir and Zanamivir are the antiviral drugs which are most likely effective in an influenza pandemic and thus many countries and the World Health Organization (WHO) have stockpiled the medications in order to mitigate against coming influenza pandemics4. However, if drug resistance towards the medications stockpiled has developed in the pandemic strain soon after delivery of antivirals, it would lead to the worst scenario where further application of antivirals would not be effective in neither treating infected patients nor controlling spreading of the virus. Essentially, the resistant strain would continue to transmit among humans.
Introducing Competition between Viral Strains by Antiviral Suspension
Upon antiviral suspension, the wild-type strains will no longer be suppressed and infections by the strains are expected to be increased. The rationale of the strategy is to raise the population of the wild-type viruses and to introduce intra-species competition for hosts between the wild-type and resistant strains. As the original dominant strain, the wild-type viruses are expected to have advantages in adaptations over the resistant strain. Thus, introducing competition between wild-type and resistant strains would result in the condition that wild-type viruses become the dominant strain and the incidence of resistant strain infection would diminish.
Mathematical Model for the Emergence of Antiviral Resistance
In order to evaluate the outcomes of antiviral suspension strategy in the scenario described above, a mathematical simulation of influenza pandemic is constructed and the efficacies of antiviral suspension will be examined. The model is based on a former study investigating the logistics of large-scale antiviral intervention during an influenza pandemic5, which follows the standard susceptible-infectious-recovered (SIR) structure.
For simplicity, we assume that there is only one fit resistant strain. At time=0, we assume all individuals are susceptible for influenza infection (S). For individuals infected with the wild-type, we first split this group into 2 compartments:, individuals who are infected and receive antiviral treatment, and , individuals who are infected but do not receive treatment. To take into account the emergence of antiviral resistance, we partition the infectious groups further with 2 more compartments:, individuals who are infected with the resistant strain and have received antiviral treatment, and , individuals who are infected with the resistant strain and have not received treatment. For the removed cases, and are individuals who have recovered or died from a wild-type infection with and without antiviral treatment, respectively. For those infected with the resistant strain, are removed individuals who have received treatment whereas are removed individuals who have not received antiviral treatment.
We assume that each infected individual receives antiviral treatment with probability α upon the onset of symptoms. In this model, represents the rate of recovery for wild-type cases who receive antiviral treatment, whereas represents the rate of recovery for untreated wild-type cases, where >.
λ is the force of infection from the wild-type cases, i.e. λ = β (+) where β is the infectivity rate for wild-type viruses. λR is the force of infection from the resistant cases where λR = (+) and is the infectivity rate for the resistant strain. The mathematical model for current simulation is illustrated in Figure 1 and the state variables and parameters are summarised in Table 1.
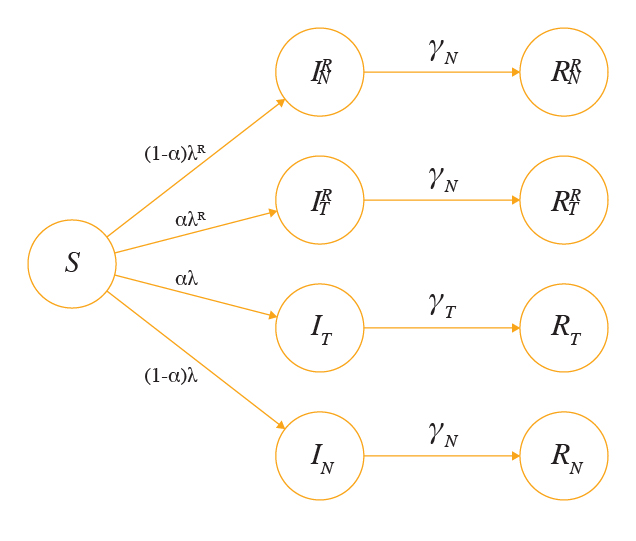
Figure 1. Summary of the basic model

Table 1. Summary of state variables and parameters
We assume that for every wild-type case treated with antiviral, there is a probability P that resistance will develop. Assuming that resistance emerges at a constant rate of θ during the infectious period, the relationship between θ and P can be expressed as
P = θ / (θ+), or θ = (•P) / (1- P)
Estimated Outcomes of Antiviral Suspension Strategy
Provided the population size of 7 million and the assumed initial number of influenza infected cases of 30, all of the initial infections are wild-type. With effective antiviral treatment, wild-type cases are assumed to recover in 1/days while those without antiviral treatment recover in 1/days. In the current simulation, we assume 1/ = 3 days and 1/ = 5 days. Referenced from the influenza pandemic in 1918, the reproductive number (Ro) for the first wave is estimated to be 1.5, whereas that for the second wave is 2 to 35. In the current simulation, the Ro is assumed to be 1.8. In this study, the outcome measures are (i) the overall attack rate, i.e. the proportion of population infected during the pandemic and is calculated by the total number of infected cases by the total population, and (ii) the proportion of cases that are resistant.
In the absence of antiviral resistance, increased proportion of treated yields decreased overall attack rate. For Ro=1.8, the estimated overall attack rate is 73% without any antiviral intervention. For treated proportion of 0.1, 0.25 and 0.4, the corresponding attack rates estimated are 70%, 65% and 59%, respectively (Figure 2).
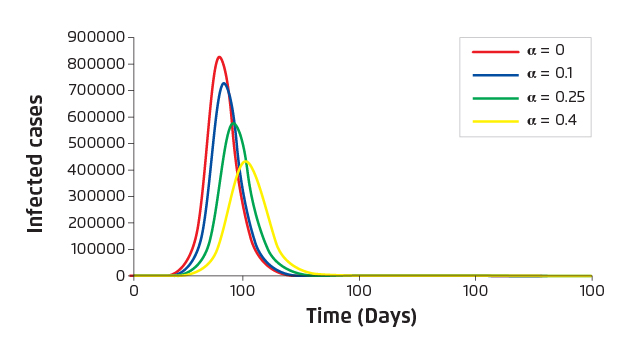
Figure 2. Estimated number of infected cases versus time
Under large-scale antiviral intervention, strong selective pressure will be imposed on the wild-type pandemic strain and resistant strain may emerge consequently. Since the pandemic strain cannot be observed until the pandemic strikes, it is impossible to predict precisely the probability of resistance emergence or the fitness cost of resistant strains. Thus, we consider a wide range of probabilities and assume that there is a single resistant strain that is fully fit. The estimated values of proportion of resistant strain infection and overall attack rate are displayed in Table 2.
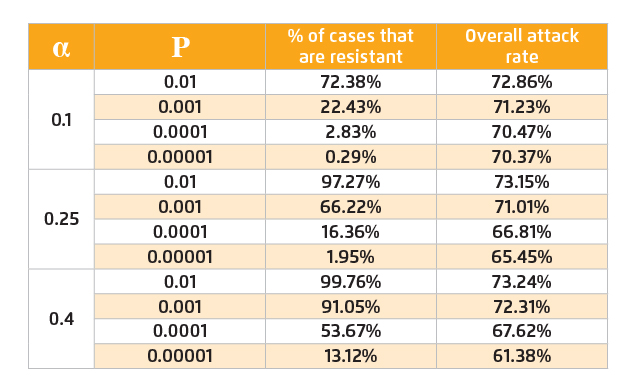
Table 2. Overall attack rates and percentages of resistant strain infection among total influenza infection
Upon the emergence of antiviral resistance, the benefits of further application of antiviral would be diminished unless P is very small. Hence, introducing intra-species competition between wild-type and resistant strains would be considered to minimise the occurrence of resistant strain infection. Antiviral suspension results in reduction of the number of resistant cases but at the same time increases the overall attack rate as a consequence of increasing the number of wild-type cases. As shown in Table 3, under most conditions, the overall attack rate will rise back to 73% due to antiviral suspension. Nonetheless, the estimated proportion of resistant strain infection drops dramatically (Figure 3).
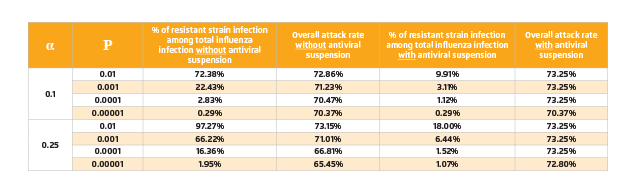
Table 3. Summary of the impact of antiviral suspension on percentages of
resistant strain infection among total influenza infection and overall attack rates
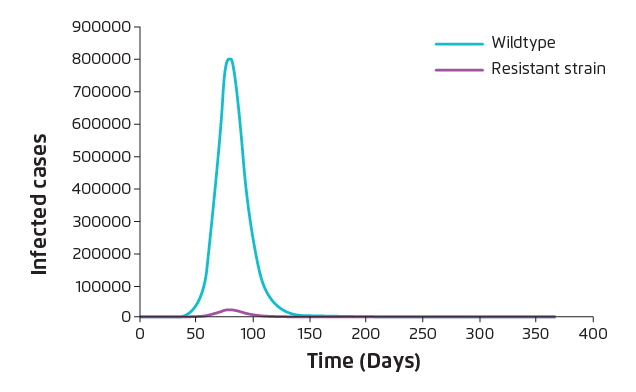
Figure 3. Reduction in Resistant strain infection upon antiviral suspension (α=0.4, P=0.0001)
Surveillance on Resistant Strain Transmission Is Essential
The spread of resistant strain is one of the main concerns during pandemics. Based on the current mathematical simulation, suspension of antiviral would lead to reduction in resistant strain infection by more than 50% with less than 8% increase in overall attack rate. Hence, suspension of antiviral treatment during a pandemic would be needed when the rate of infection is positive (Note: any change in treatment protocol is not recommended when rate of infection is negative as the pandemic is declining), and the rate of spread of resistant strain is greater than that of wild-type. However, health policy decision makers should keep monitoring the spread of resistant strain in the surveillance period and estimate the transmissibility of the resistant strain. In case when suspension of antiviral intervention is needed, decision makers should make a balance between overall attack rate and percentage of resistant strain infection in their pandemic planning. Of importantly, appropriate public health interventions including quarantine strategies, resources allocation, proposal of travel restrictions and prophylaxis strategies are essential in facilitating recovery of patients and reducing secondary infection during pandemics.
References
1. Mei et al. Drug Discov Ther. 2013;7(3):95-100. 2. Wolf et al. Biol Direct. 2006;1. 3. Parrish et al. Annu Rev Microbiol. 2005;59(1):553-586. 4. Patel et al. Am J Infect Control. 2017;45(3):303-305. 5. Arinaminpathy et al. J R Soc Interface. 2008;5(22):545-553.